BLOQUE 2

FUNCIONES CUADRÁTICAS

La idea de cuadrático, por otra parte, también se usa en el ámbito de las matemáticas, aludiendo a aquello relacionado con el cuadrado (el producto de la multiplicación de una cantidad por sí misma).

EJEMPLOS:

1.

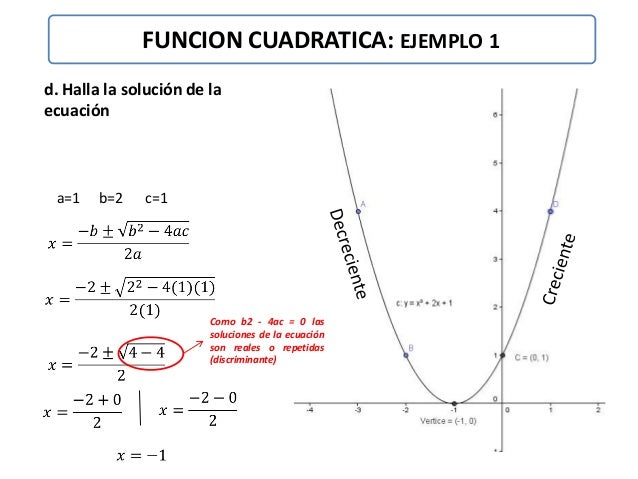
2.

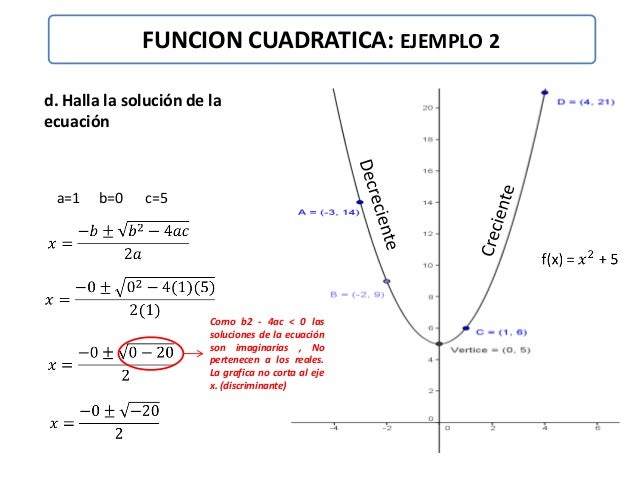
VÍDEO:

MODELO GRÁFICO

EJEMPLO:

1.

2.

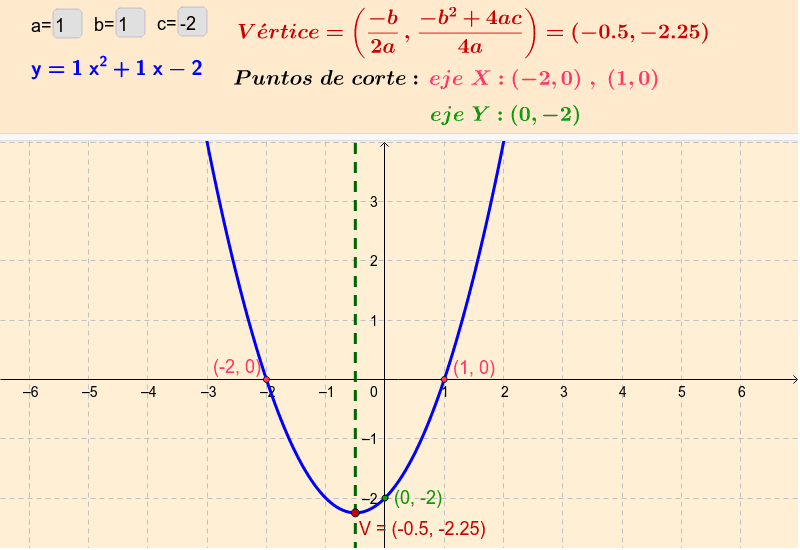
3.

VÍDEO:

RAÍCES Y EL DISCRIMINANTE

EJEMPLO:

1.

2.

3.

VÍDEO:

FORMAS ESTÁNDAR Y FACTORIZADA

Toda función cuadrática se puede factorizar en función de sus raíces. 

Dada:

    

se puede factorizar como:

    siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x² sería siempre 1. x₁ y x₂ representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x₁ = x₂ .

 

 

  

EJEMPLOS:

1.

2.

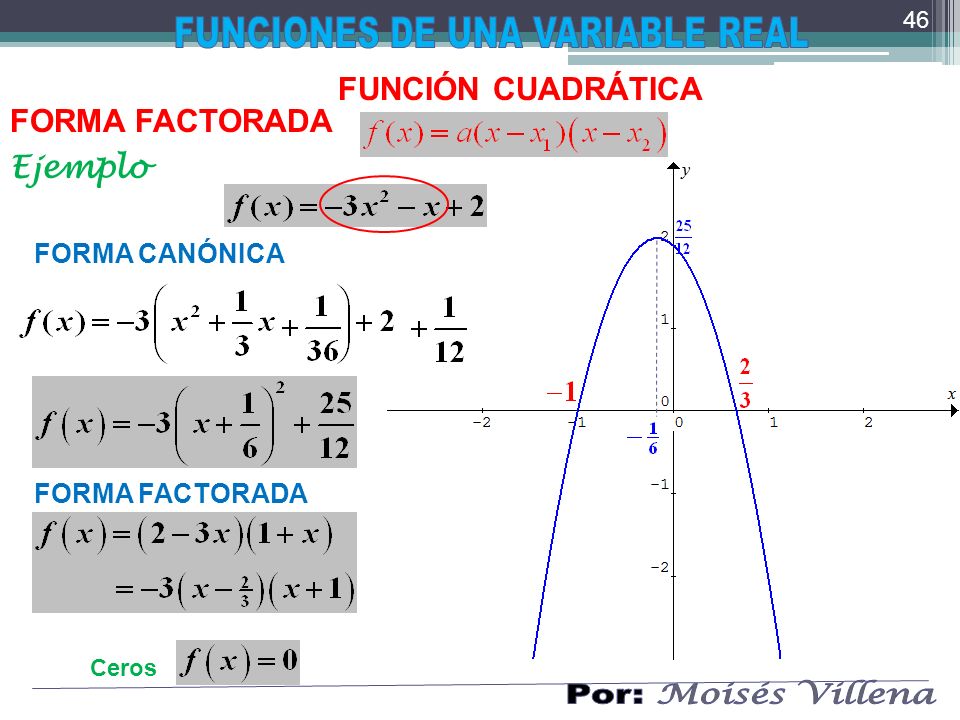
3.

VÍDEO:

FUNCIONES DE GRADO SUPERIOR 

La expresión de una función polinomial es: donde n es un numero real entero no negativo, al igual que cada una de las constantes a. El grado del polinomio es n y su coeficiente de mayor grado, o sea, an, es su coeficiente principal.

EJEMPLOS:

1.

2.

3.

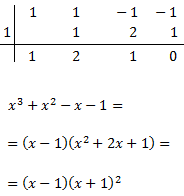
VÍDEO:

MODELO GRÁFICO

Función polinomial de tercer grado. La función polinomial de tercer grado es toda aquella función que se puede escribir de la forma:y = a3x3 + a2x2 + a1x + a0
donde a3 6= 0.La función polinomial de tercer grado también se conoce como función cúbica.

EJEMPLOS:

1.

2.

3.

VÍDEO:

RAÍCES: TEOREMA DEL RESIDUO, DEL FACTOR Y DIVISIÓN SINTÉTICA.

Si se divide la función polinomial ƒ(x) entre el binomio x - a donde a es un número real, el residuo es igual a ƒ(a). 

El teorema del residuo indica que el resultado de evaluar numéricamente una función polinomial para un valor a es igual al residuo de dividir el polinomio entre x - a. Un ejemplo de esto se ilustra en la parte de arriba. Se recomienda que el lector realice otras comprobaciones. Una conclusión muy importante del teorema del residuo es se puede evaluar numéricamente una función polinomial usando la división sintética. 

EJEMPLOS:

1.

x³ + 2x² - 3x + 5 entre x - 2

En este caso, a=2 y por lo tanto sustituimos "a" en el polinomio:

(2)³ + 2(2)² - 3(2) + 5 = 8 + 8 - 6 + 5 = 15


El residuo es entonces 15.


2.
(x3 − 5x − 1) tiene por factor (x − 3)
(x3 − 5x −1) es divisible por (x − 3) si y sólo si P(x = 3) = 0.
P(3) = 33 − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0

(x − 3) no es un factor.

3.
(x4 − 2x3 + x2 + x − 1) tiene por factor (x − 1)
(x4 − 2x3 + x2 + x − 1) es divisible por (x − 1 ) si y sólo si P(x = 1) = 0.
P(1) = 14 − 2 · 13 + 1 2 + 1 − 1 = 1 − 2 + 1 + 1 − 1 = 0

(x − 1) es un factor.

VÍDEO:

TRATAMIENTO VISUAL DE MÁXIMOS Y MÍNIMOS

La determinación de los valores máximos y mínimos de una función, es uno de los logros de la gran potencia que tiene el Cálculo. Tomemos f(x) como una función de x. El valor de x para el cual la derivada de f(x) con respecto a x es igual a cero, corresponden a los puntos de inflexión de la función f(x) donde sus valores son máximo y mínimo.

EJEMPLOS:

1.

2.

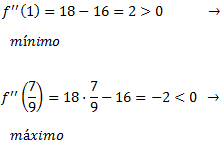
3.

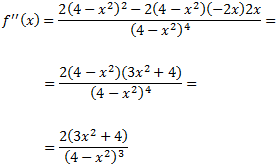
VÍDEO:

BLOQUE 3

FUNCIÓN RACIONAL

En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma:

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo, esta fracción es irreducible, es decir que las ecuaciones P(x) = 0 y Q(x) = 0 carecen de raíces comunes. Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos

EJEMPLOS:


1.

2.

3.

VÍDEO:

MODELO ALGEBRAICO GENERAL DE UNA FUNCIÓN RACIONAL

EJEMPLOS:

1.

2.

3.

VÍDEO:

MODELO GRÁFICO

Las gráficas de las funciones racionales pueden ser difíciles de dibujar. Para dibujar una gráfica de una función racional, puede comenzar encontrando las asíntotas y las interrupciones.

Pasos involucrados para graficar las funciones racionales:

Encuentre las asíntotas de la función racional, si las hay.

Dibuje las asíntotas como rectas punteadas.

Encuentre la intercepción en x y la intercepción en y de la función racional, si las hay.

Encuentre los valores de y para varios valores diferentes de x .

Grafique los puntos y dibuje una curva lisa que conecte los puntos. Asegúrese que la gráfica no cruce las asíntotas verticales.

EJEMPLOS:

1.

2.

3.

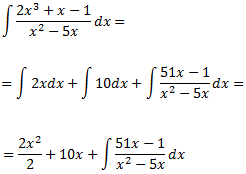
VÍDEO:

ASINTOTAS

Una asíntota es una recta que se acerca a la gráfica de la función, pero nunca la toca. En la función padre   , tanto los ejes x y y son asíntotas. La gráfica de la función padre se acercará más y más pero nunca tocará las asíntotas.

Una función racional de la forma   tiene una asíntota vertical en el valor excluido, o x = b , y una asíntota horizontal en y = c .

EJEMPLOS:

1.

2 x + 1 = 0

x = -1/2

La asíntota vertical de la función racional es x = -0.5.

2.

Esta función tiene la intercepción en x en (-1/4, 0) y la intercepción en y en (0, 1). Encuentre más puntos en la función y grafique la función.

3.

Por ejemplo, la función racional   tiene un hoyo en x = 0.

VÍDEO: