BLOQUE 1

RELACIONES Y FUNCIONES 

IN-ECUACIONES :

Denomina in-ecuación a una desigualdad algebraica en la cual sus miembros se encuentran vinculados por los signos < (menor que), ≤ (menor o igual que), > (mayor que) o ≥ (mayor o igual que). De esta manera, las in-ecuaciones se expresan del siguiente modo:

f(x) < g(x) o

f(x) ≤ g(x) o

f(x) > g(x) o

f(x) ≥ g(x)

EJEMPLOS:

1.

3x − 4 < 8 3x < 12 x < 4

2.

En cambio, si tomamos el valor 5:
3 x 5 – 4 < 8 
15 – 4 < 8 
11 < 8 (lo cual no es correcto: 11 no es menor que 8)

3.

3 x 3 – 4 < 8
9 – 4 < 8
5 < 8
o
3 x 2 – 4 < 8
6 – 4 < 8 

2<8

VÍDEO:

RELACIONES Y FUNCIONES

Una Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Imagen , de manera que a cada elemento del Dominio le corresponde uno o más elementos del conjunto Imagen. Por su parte, una Función aplicación   es una relación entre un conjunto de partida X denominado dominio y un conjunto de llegada Y denominado imagen   de forma que a cada elemento x del dominio le corresponde un único elemento imagen f(x). Se denota por: f: X→ Y.

EJEMPLOS:

1.

2.

3.

VIDEO:

DOMINIO Y RANGO:

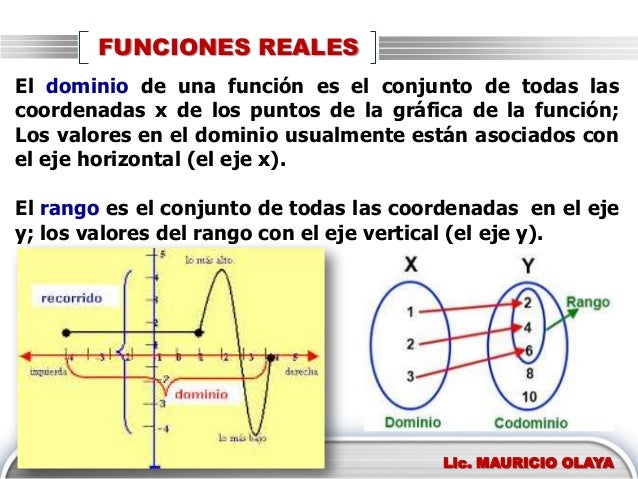
EJEMPLOS:

1.

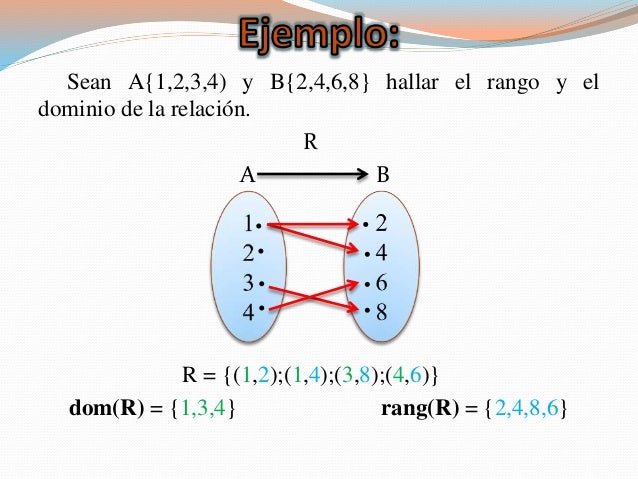
2.

EJERCICIO:

VÍDEO:

IMAGEN DE UNA FUNCIÓN

A la imagen de una función también se le puede llamar recorrido o rango.
Dicho con otras palabras, son los valores de f(x) en los que existe la función.

EJEMPLOS:

1.

2.

VÍDEO:

REGLA DE CORRESPONDENCIA

Una regla de correspondencia consiste en asignar un elemento único de un cierto conjunto a cada elemento único de otro conjunto. 

EJEMPLOS:

1.

Tomemos un conjunto A, que está formado por 3, 4 y 5, y un conjunto B, el cual está compuesto por 9, 12 y 15. La correspondencia entre ambos es el triple. De este modo, la regla de correspondencia permite vincular cada elemento del Dominio (el conjunto A) a un elemento del Codominio (el conjunto B).

f(x) =3x

f(3) = 3×3 = 9

f(4) = 3×4 = 12

f (5) = 3×5 = 15

2.

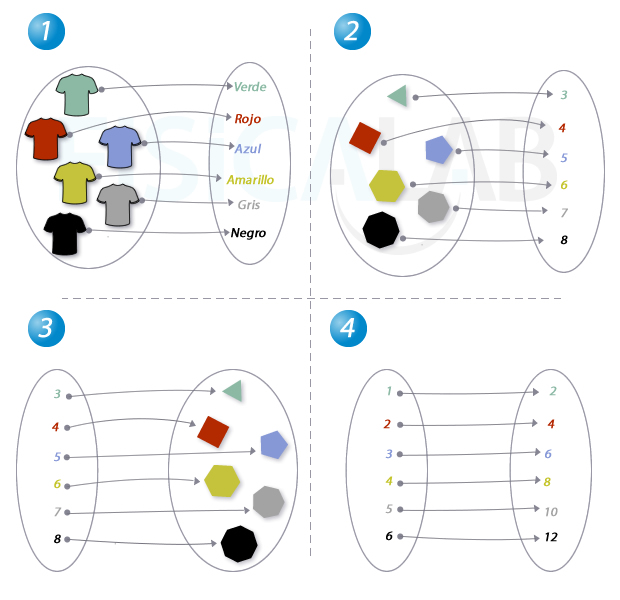
3.

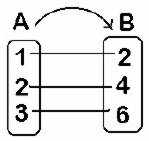
VÍDEO:

GRAFICACION DE FUNCIONES:

FUNCIONES ESPECIALES:

Una función especial es una función matemática particular, posee nombres y designaciones más o menos establecidos.
No existe una definición general de las mismas, pero la lista de funciones matemáticas contiene funciones que son generalmente aceptadas como especiales. En particular, las funciones elementales son también consideradas funciones especiales.

EJEMPLOS:

1.

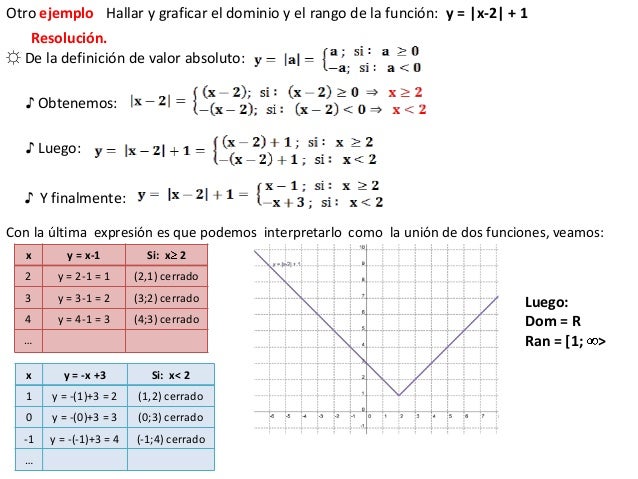
2.

3.

VÍDEO:

FUNCIÓN INVERSA

Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b , entonces f−1(b) = a.

Cálculo de la función inversa

1. Se escribe la función con x e y.

2. Se despeja la variable x en función de la variable y.

3. Se intercambian las variables.

EJEMPLOS:

1.

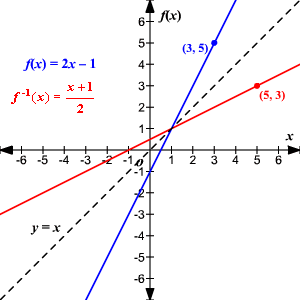
2.

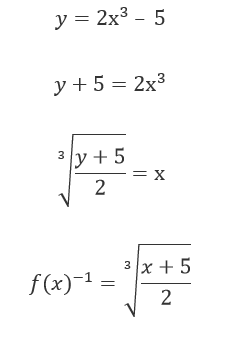
3.

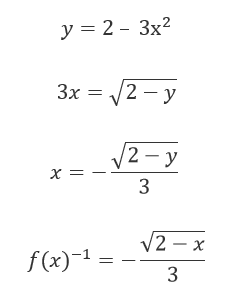
VÍDEO:

FUNCIONES CRECIENTES Y DECRECIENTES

· Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x₁  y x₂, con la condición x₁ £ x₂, se verifica que
 f( x₁ ) < f( x₂ ).
 Se dice estrictamente creciente si de x₁ < x₂ se deduce que f(x₁) < f(x₂).
   · Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x₁  y x₂, que cumplan x₁ £ x₂, entonces f(x₁ ) ³ f(x₂ ).
Siempre que de x₁ < x₂ se deduzca f(x₁ ) > f(x₂ ), la función se dice estrictamente decreciente.

EJEMPLOS:

1.

2.

3.

VÍDEO:

TRANSFORMACIONES GRÁFICAS

  Las gráficas de las siguientes funciones f(x)=x, f(x)=x² y f(x)=׀x׀ las conocemos. Cada una de ellas tiene una forma particular y sabemos cual es su forma general. Estas se dibujan utilizando técnicas aplicadas a los modelos gráficos de cada función llamadas transformaciones. Estas transformaciones afectan la forma general de la gráfica de cada función. Las traslaciones, reflejos y las expansiones - compresiones son las transformaciones a estudiar.

EJEMPLOS:

1.

Utilizar la gráfica de f(x)=x2 para bosquejar la gráfica de y = f(x) + 2 y y = f(x) - 2. 

 Solución:

Ejemplo Traslacion Vertical

    La gráfica de f(x)=x2 se llamará gráfica de la función modelo. Los puntos principales de la gráfica de esta función son; (-1, 1), (0, 0) y (1, 1).

    La gráfica de y =f(x) + 2 es la gráfica modelo desplazada dos unidades hacia arriba. Por lo tanto en los puntos desplazados cambian las y, los nuevos puntos se obtienen sumando 2 a las y. Los nuevos puntos son; (-1, 3), (0, 2) y (1, 3).

    La gráfica y= f(x) - 2 es la gráfica de la función modelo desplazada dos unidades hacia abajo. Por lo tanto en los puntos desplazados cambian las y, los nuevos puntos desplazados se obtienen restando dos a las y. Los nuevos puntos son; (-1, -1), (0, -2) y (1, -1).

2.

Utilizar la gráfica de f(x)=x2 para bosquejar la gráfica de y = f(x-2) y y = f(x+4). 

Solución:

Ejemplo Traslacion Horizontal

  La gráfica de f(x)=x2 se llamará gráfica de la función modelo . Los puntos principales de esta función son; (-1, 1), (0, 0) y (1, 1).

  La gráfica de y =f(x-2) es la gráfica modelo desplazada dos unidades hacia la derecha. Por lo tanto en los puntos desplazados cambian las x, los nuevos puntos se obtienen sumando 2 a las x. Los nuevos puntos son; (1, 1), (2, 0) y (3, 1).  

  La gráfica y= f(x+4) es la gráfica de la función modelo desplazada cuatro unidades hacia la izquierda. Por lo tanto en los puntos desplazados cambian las x, los nuevos puntos desplazados se obtienen restando cuatro a las x. Los nuevos puntos son; (-5, 1), (-4, 0) y (-3, 1).

3.

Utilizar la gráfica de f(x) = √(x) para bosquejar la gráfica de y = -f(x) y y = f(-x).

Solución:

Ejemplo Reflejos

  La gráfica de f(x)=√(x) se llamará gráfica de la función modelo . Los puntos principales de esta función son; (0, 0) y (1, 1).

   La gráfica de y = -f(x) es la gráfica modelo reflejada con respecto al eje de x. Por lo tanto en los puntos reflejados cambian las y, los nuevos puntos se obtienen buscando el opuesto de las y. Los nuevos puntos son; (0, 0) y (1, -1).  

   La gráfica y = f(-x) es la gráfica de la función modelo reflejada con respecto al eje de y. Por lo tanto en los puntos reflejados cambian las x, los nuevos puntos desplazados se obtienen buscando el opuesto de las x. Los nuevos puntos son; (0, 0) y (-1, 1).

VÍDEO:

COMPOSICIÓN DE FUNCIONES

ES EL CONJUNTO DE LAS FUNCIONES REALES DE VARIABLE REAL PODEMOS DEFINIR OTRA OPERACIÓN TOTALMENTE DISTINTA LLAMADA COMPOSICIÓN DE FUNCIONES.

EJEMPLOS:

1.

2.

VÍDEO

BLOQUE 2

MODELO ALGEBRAICO GENERAL DE FUNCIONES POLINOMIALES

FUNCIÓN LINEAL

Una función lineal es una función polinómica de primer grado, es decir, una función cuya representación en el plano cartesiano es una línea recta.

EJEMPLOS:

1.

2.

3.

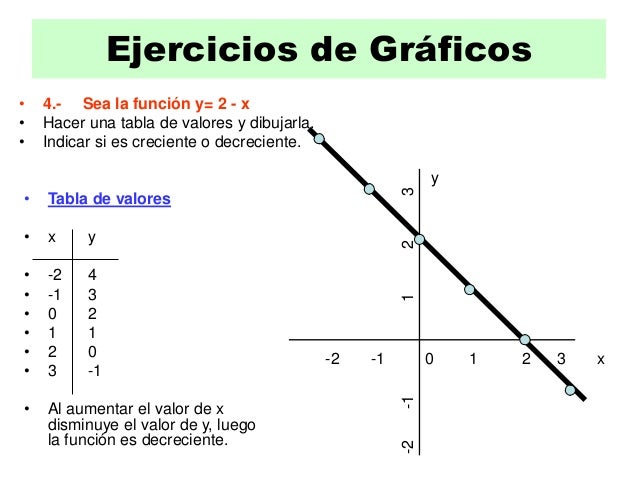
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
en esta recta el parámetro ${\displaystyle m}$ es igual a ${\displaystyle {\frac {1}{2}}}$ (corresponde al valor de la pendiente de la recta), es decir, cuando aumentamos ${\displaystyle x}$en una unidad entonces ${\displaystyle y}$ aumenta en ${\displaystyle {\frac {1}{2}}}$ unidad, el valor de ${\displaystyle b}$ es 2, luego la recta corta el eje ${\displaystyle y}$ en el punto ${\displaystyle y=2}$.
En la ecuación:
la pendiente de la recta es el parámetro ${\displaystyle m=-1}$, es decir, cuando el valor de ${\displaystyle x}$ aumenta en una unidad, el valor de ${\displaystyle y}$disminuye en una unidad; el corte con el eje ${\displaystyle y}$ es en ${\displaystyle y=5}$, dado que el valor de ${\displaystyle b=5}$.
En una recta el valor de ${\displaystyle m}$ corresponde al ángulo ${\displaystyle \theta }$ de inclinación de la recta con el eje de las ${\displaystyle x}$ a través de la expresión:
.

VÍDEO

MODELO GRÁFICO

El método gráfico para resolver este tipo de sistemas consiste, por tanto, en representar en unos ejes cartesianos, o sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resume en las siguientes fases:
Se despeja la incógnita y en ambas ecuaciones.
Se construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
Se representan gráficamente ambas rectas en los ejes coordenados.

EJEMPLOS:

1.

2.

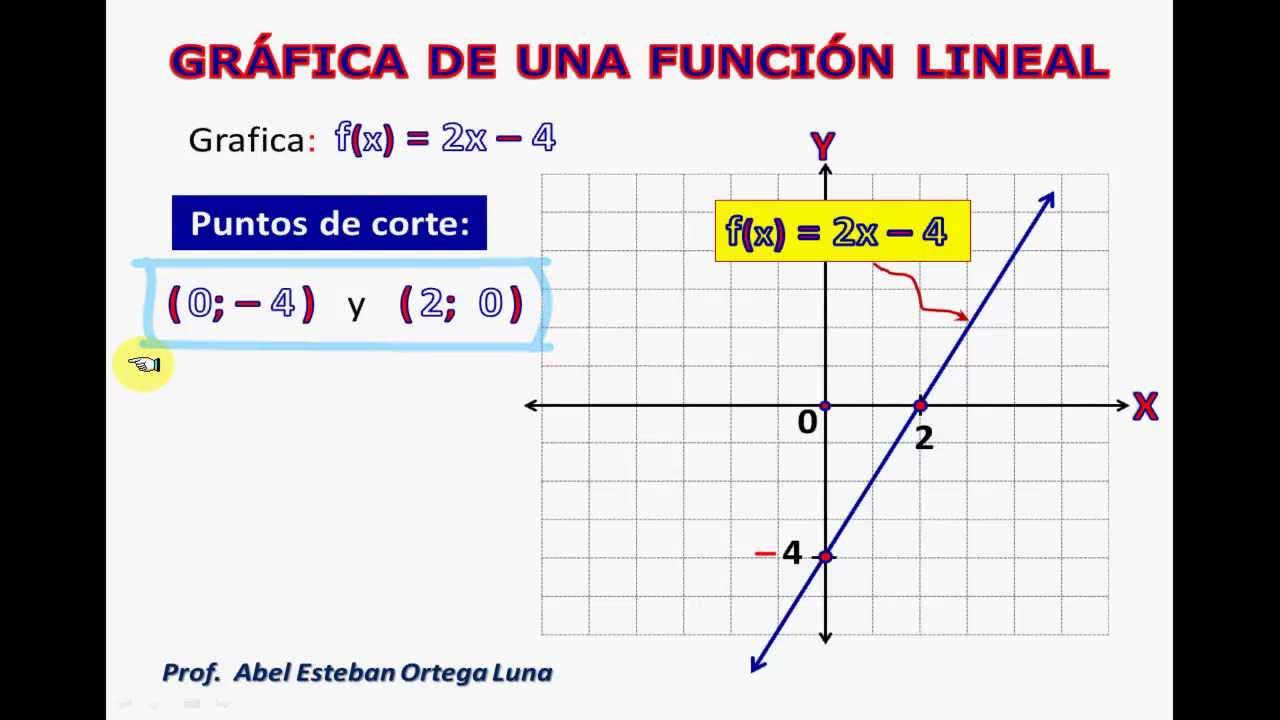
VÍDEO

MODELO ALGEBRAICO

EJEMPLOS:

1.

2.

VÍDEO

RAÍCES

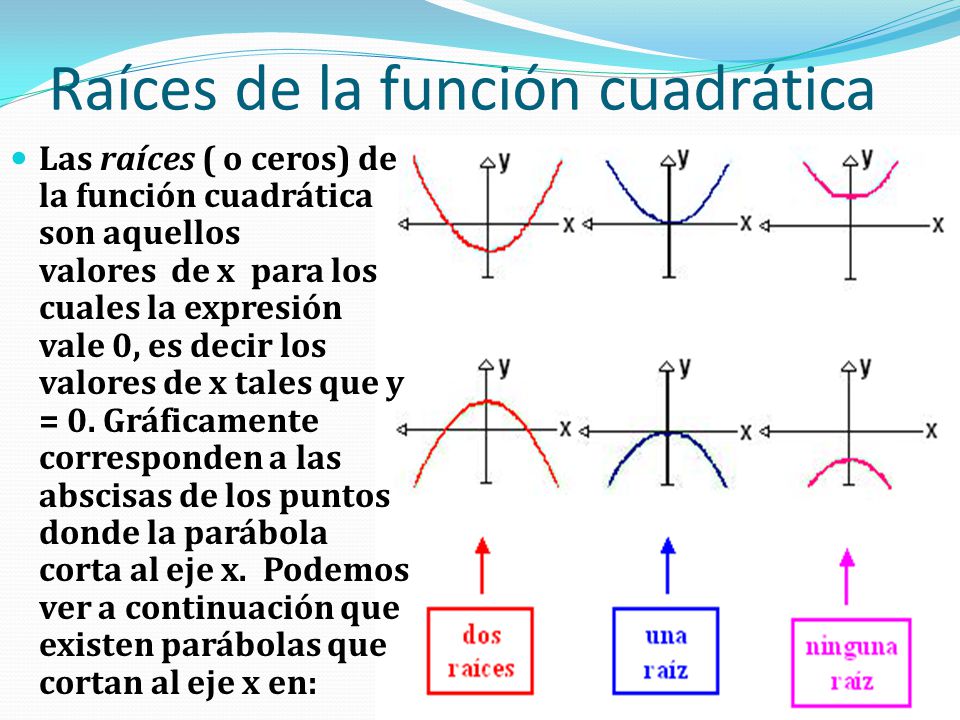
EJEMPLOS:

1.

2.

3.

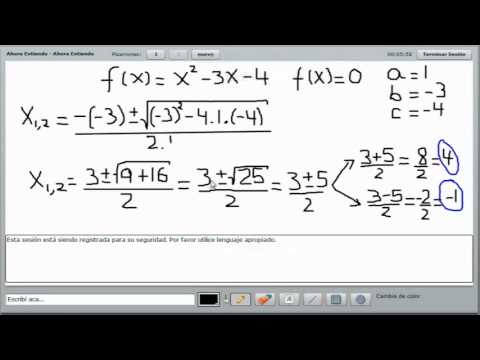
VÍDEO

BLOQUE 2

FUNCIONES CUADRÁTICAS

La idea de cuadrático, por otra parte, también se usa en el ámbito de las matemáticas, aludiendo a aquello relacionado con el cuadrado (el producto de la multiplicación de una cantidad por sí misma).

EJEMPLOS:

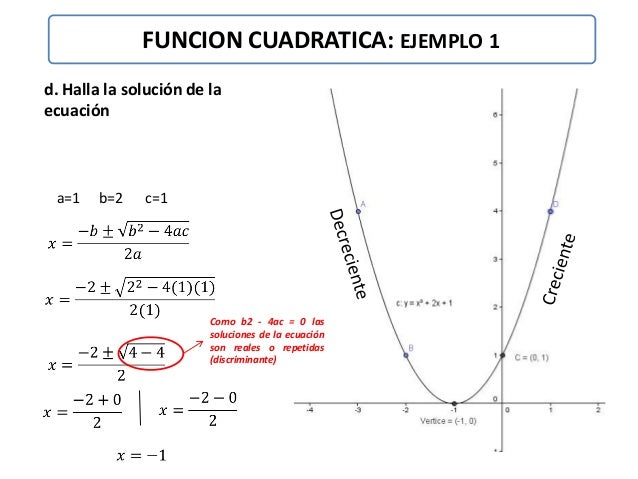
1.

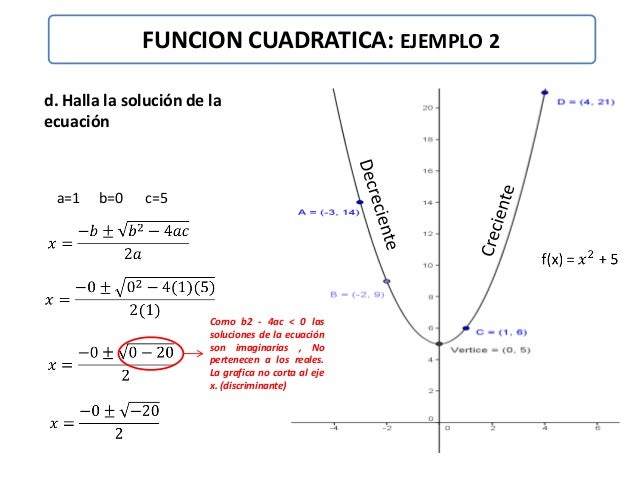
2.

VÍDEO:

MODELO GRÁFICO:

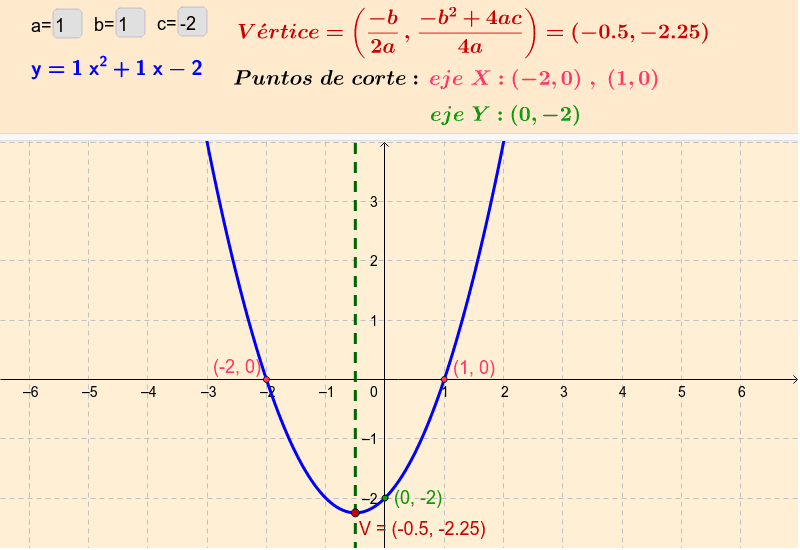
Uno de los métodos para resolver las ecuaciones cuadráticas es la graficación, donde tenemos que encontrar la variable independiente (x) y la variable dependiente (y).
Pero para hacer esto debemos primero de ubicar las ecuaciones cuadrática

EJEMPLO:

1.

2.

3.

VÍDEO:

RAÍCES Y EL DISCRIMINANTE

Una ecuación cuadrática puede tener dos raíces, una raíz, o ninguna raíz. En la fórmula cuadrática, la expresión bajo el símbolo radical determina cuántas soluciones tendrá la fórmula. Esta expresión , , se llama el discriminante de la ecuación 

1.

2.

3.

VÍDEO:

FORMAS ESTÁNDAR Y FACTORIZADA