Tercer parcial

BLOQUE 3

APROXIMACIÓN INFORMAL A LOS LIMITES.

DEFINICIÓN:

Para estudiar el límite de una función racional, se distinguirán dos casos:

Puesto que una función racional es el cociente de dos polinomios, para calcular su límite puede aplicarse la regla para el cálculo del límite de un cociente de dos funciones:

                                         

Tanto el límite del numerador como el del denominador son límites de funciones polinómicas, cuyo cálculo se explicó en el apartado anterior.

Al efectuar estos límites pueden darse varias situaciones.

Se calculan en este caso los límites de P(x) y Q(x) como funciones polinómicas y se halla su cociente.

_EJEMPLOS:

1.

Resolución:

2.

Resolución:

Esta indeterminación se resuelve simplificando el cociente. Aplicando la regla de Ruffini, se obtiene la descomposición de los polinomios P(x) = x³ - 2x² - 6x +12 y

Q(x) = x² + 3x -10.

Descomposición factorial de P(x):

 

· Descomposición factorial de Q(x):

 

3. 

Resolución:

VÍDEO_:

 

 FUNCIÓN EXPONENCIAL.

FORMULA GENERAL DE LA FUNCIÓN EXPONENCIAL.

DEFINICIÓN:

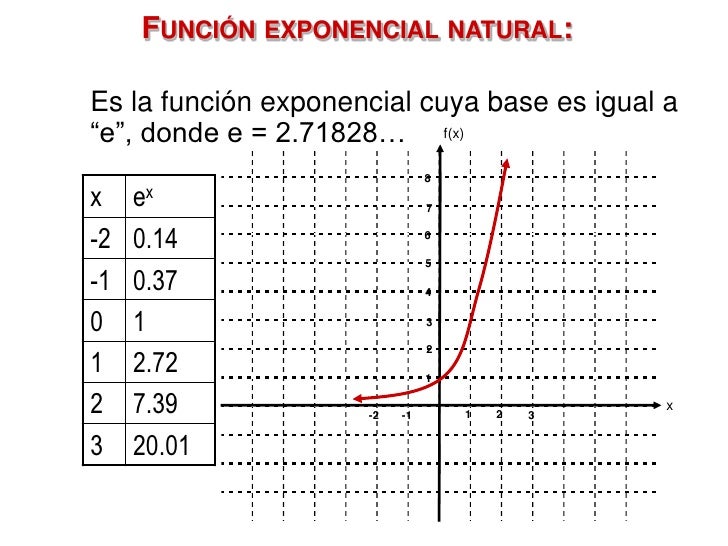
Además de funciones lineales, cuadráticas, racionales y radicales, existen las funciones exponenciales. Las funciones exponenciales tienen la forma f(x) = b^x, donde b > 0 y b ≠ 1. Al igual que cualquier expresión exponencial, b se llama base y x se llama exponente.

EJEMPLOS:

1.

2.

3.

VÍDEO_:

MODELO GRÁFICO

DEFINICIÓN:

En primer lugar, comenzar con las propiedades de la gráfica de la función exponencial de base de una base,

f (x) = a^x , a > 0 y no es igual a 1.

El dominio de la función f es el conjunto de todos los números reales. El rango de f es el intervalo (0, + infinito).

La gráfica de f tiene una asíntota horizontal dada por y = 0. Función f tiene interceptar ay en (0, 1). f es una función creciente si a es mayor que 1 y una función decreciente si a es menor que 1.

_EJEMPLOS:

_1.

2.

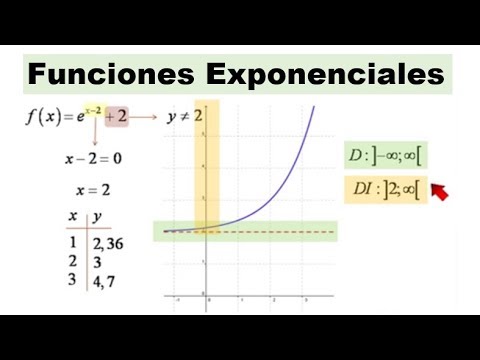
 f es una función dada por 

f (x) = 2 ^{(x - 2)}

^{El dominio de f es el conjunto de todos los números reales. Para encontrar el rango de f, empezamos con}

2 ^x > 0

^{Multiplica ambos lados por 2 -2 lo cual es positivo}

^3.
VÍDEO:

FUNCIÓN LOGARÍTMICA

DEFINICIÓN

Una función logarítmica está formada por un logaritmo de base a, y es de la forma:

siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.
Cuando 0 < a < 1, entonces la función logarítmica es una función decreciente y cuando a > 1, entonces es una función creciente.

EJEMPLOS:

1.

2.                                                                  

3.

VÍDEO:

FORMA GENERAL DE LA FUNCIÓN LOGARÍTMICA

DEFINICIÓN:

Definíamos por tanto el logaritmo en una cierta base "b" de un número "a" como el exponente al que hay que elevar la base b para obtener el número a.

Esto nos relaciona la función logarítmica con la exponencial. También lo veremos posteriormente de forma gráfica.

También sabremos que la base (b) de los logarítmos debe ser un número positivo (al igual que la base de la potencia de una función exponencial) y además no debe ser 1 ya que log₁(a) en general no existe ya que si a no es 1 1ⁿ no puede ser a.

EJEMPLOS:

1. 

2.

3.

VÍDEO:

MODELO GRÁFICO

DEFINICIÓN:                                            

La función   es la función inversa de la función exponencial .
Considere la función  . Puede graficarse como:

EJEMPLO:                                            

1.

La gráfica de la función inversa de cualquier función es la reflexión de la gráfica de la función sobre la recta  . Así, la gráfica de la función logarítmica  que es la inversa de la función  es la reflexión de la gráfica anterior sobre la recta  .

2.

Cuando ninguna base se escribe, se asume que el log es base 10.

3.

Ahora,  . La gráfica de  será desplazada 3 unidades hacia abajo para obtener  .

^VÍDEO: 

PROPIEDADES DE LOS LOGARITMOS.

DEFINICIÓN:

En tus estudios del álgebra, te has topado con muchas propiedades, como la conmutativa, la asociativa y la distributiva. Estas propiedades te ayudan a simplificar una expresión o una ecuación complicada.

Lo mismo sucede con los logaritmos. Hay un grupo de propiedades que te ayudan a simplificar expresiones complejas de logaritmos. Como los logaritmos se relacionan estrechamente con las expresiones exponenciales, no es de sorprender que las propiedades de los logaritmos se parezcan a las propiedades de los exponentes. Como un recordatorio, aquí están las propiedades de los exponentes.

^EJEMPLOS:                                                  

^{1.                                                                 
2.                                                                 
3.                                                                   
VÍDEO:}                                                   

^{CAMBIO DE BASE
DEFINICIÓN:}                                         

  El cambio de base logoritmo se utiliza para cambiar la base de logaritmos. El cambio de la fórmula baja es.

Cuando los logaritmos primero fueron inventados, no había calculadoras. Los matemáticos y los astrónomos utilizaron los libros publicados con las tablas de logaritmos. Cada tabla tenía exactamente una base

                                   <sup>EJEMPLOS:    1.

2.
3.
VÍDEO:</sup>                                           

ECUACIONES EXPONENCIALES Y LOGARÍTMICAS

FUNCIONES TRIGONOMÉTRICAS 

FORMA GENERAL Y CARACTERÍSTICAS DE LAS FUNCIONES TRIGONOMÉTRICAS

DEFINICIÓN:

Lo importante a destacar es que el ángulo en todos los casos es el mismo.

Este hecho es importante ya que permite relacionar a los ángulos con la razón de la proporción de los lados. Esta relación presenta la propiedad de unicidad y la propiedad de completitud (para cada par de lados homólogos existe siempre un único valor (razón) relacionado con una determinada [existe y es única] amplitud angular), por lo tanto se establece una función, a las que llamaremos trigonométrica.

<sup>EJEMPLOS:
1.
2.

3.
VÍDEO:</sup>

^{MODELO GRÁFICO
DEFINICIÓN:}                                    

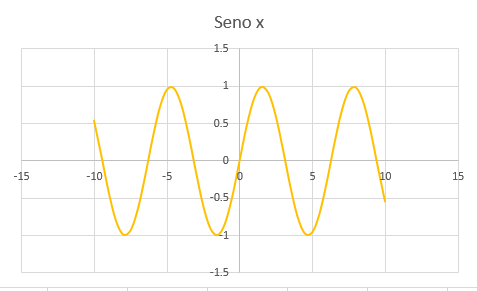
 Las gráficas de las funciones trigonométricas  poseen propiedades matemáticas muy interesantes como máximo, mínimo, asíntotas verticales, alcance y periodo entre otras.Es necesario estudiar la forma de la gráfica de cada función trigonométrica. Esta forma está asociada a las características particulares de cada función. En la figura de abajo se presentan algunas gráficas de funciones trigonométricas.

EJEMPLOS:

1.

2.

3.

race la gráfica de la función f(x) = 2cos(x-π/6) + 1.

Solución:

Características: El alcance es el conjunto de imágenes correspondientes al intervalo [-1, 3]. El ciclo fundamental no interseca el eje de y. Tiene máximo en los puntos (π/6, 3) y (13π/6, 3) y el mínimo en el punto (7π/6, -1) . VÍDEO: